Marque o painel frontal. Escala universal.
Parte 1. Por que escala "universal"?
Eu precisava dividir um espaço em branco redondo em 7 partes. Eu tentei dividir 360 por 7. E daí? Não é dividido sem deixar rastro! E imediatamente a pergunta: como a escala no painel frontal, marcada em 360 partes, pode me ajudar? divisão por um grau? Resposta: de jeito nenhum.
Portanto, a idéia veio para marcar o painel frontal com a aplicação de uma escala universal. A idéia é colocar mais 4 escalas na escala principal.
A escala principal, vamos chamá-lo assim, é o layout do painel frontal em 15 graus. No painel frontal, fazemos as marcas "0", "90", "180" e "270". Então, em ambos os lados de cada uma das marcas, colocamos riscos com diferentes valores de divisões. Portanto, em um setor de 330 a 30 graus ("0" ou "360" no meio), colocaremos uma escala de 60 divisões, ou seja, uma divisão será igual a 6 graus.
Em um setor entre 60 e 120 graus ("90" no meio), coloque uma escala de 48 divisões, ou seja, uma divisão será igual a 7,5 graus.
No setor de painel frontal, entre 150 e 210 graus (“180” no meio), marcamos a escala em 42 divisões, ou seja, o preço de uma divisão é 8,75 graus.
No setor da placa entre 240 e 300 graus ("270" no meio), colocaremos uma escala de 36 divisões, ou seja, com um preço de divisão de 10 graus.
E agora existem poucos argumentos a favor de uma ruptura desse painel.
1. Usando a escala "42", podemos dividir o círculo em 7 partes, porque 42 é dividido por 7 sem deixar resto - são 6 divisões. Assim, com sua ajuda, você pode dividir o círculo em 14, 21, 42 partes. Uma escala de 360 partes não permitirá isso.
2. Ao dividir o painel em 360 divisões, podemos dividir em 2, 3,4,5,6,8,9,10,12,15, 18,20,24,30,36,40,45,60,90,120 divisões e apenas 21 valores.
A escala universal, além desses valores, permitirá decompor vários outros valores: 7, 14, 16, 21, 48, 72, 80, 144, 240. Ou seja, em 30 valores, pelo menos.
Consequentemente, a escala universal é mais funcional que a escala de 360 divisões.
Parte 2. Um pouco sobre a teoria dos erros.
Temos que aceitar pelo axioma que qualquer medição (!!!) podemos fazer apenas com um erro. Ou, caso contrário, é praticamente impossível realizar qualquer medição sem erros.
A precisão da medição é influenciada por vários fatores. Listamos alguns deles.
1. Qualquer ferramenta de medição é diferente da referência.
2. Qualquer curso tem dimensões lineares reais.Por exemplo, a ponta de uma agulha de bússola tem uma "espessura" de vários mícrons, bem, por exemplo 10. Ao combinar uma régua com esse golpe, não podemos "a olho" determinar em qual parte do golpe a borda da régua cai: um, segundo ou terceiro mícron de espessura.
3. O lápis mais afiado também possui uma espessura de cerca de 0,2 mm, além disso, a cada golpe, essa espessura muda devido à abrasão da grafite.
Conclusão: para necessidades práticas em casa condições, podemos "confiar" na precisão de alguns centésimos de milímetro.
Com base nas considerações acima, as agulhas mais afiadas, as réguas planas, as mãos limpas e os olhos atentos devem ser usados ao marcar o painel frontal.
Parte 3. Marcação.
Para marcar, fiz uma moldura com pedaços de barras, um pedaço de papelão. A estrutura foi presa à máquina com grampos, enquanto o plano da tela (folha de papelão com uma folha de papel) deve estar perpendicular às guias da máquina. E mais um requisito: a tela deve estar localizada não apenas perpendicularmente, mas também para que a régua, montada em um eixo no mandril da máquina, deslize pela tela sem folga. Esse arranjo é necessário para a máxima eliminação possível de erros de marcação.
Preste atenção ao fato de que nossa régua improvisada de acabamento em zinco também se encaixa perfeitamente no painel frontal, e a parte "de trabalho" (a parte pela qual desenharemos riscos) deve ser perpendicular ao plano do painel frontal. Em vez de cortar a galvanização, você pode, é claro, pegar uma régua de metal. Mas a guarnição pode ser facilmente dobrada para se encaixar bem no painel frontal. Protegido com uma carga. Eu tenho esse disco de metal.
A linha do canto tem cinco orifícios, todos localizados na mesma linha. Um orifício com um diâmetro de 5,8 mm. Um grampo de cabelo de 6 mm é inserido nele, o qual é preso com porcas dos dois lados. Os quatro furos a seguir foram perfurados com uma broca de 1 mm e estão localizados no eixo do primeiro furo, respectivamente 195 (para 36 divisões), 220 (para 60), 241 (para 42), 260 (para 48 divisões) mm. Por experiência, direi que a broca deve ser tomada duas vezes mais fina - 0,4 - 0,5 mm. Mas eu não tinha em mãos. O fato é que vamos inserir um lápis afiado nesses orifícios e, girando a régua, desenharemos arcos do raio correspondente. A ponta de um lápis em um buraco com um diâmetro de 1 mm trava um pouco, isto é, o raio é desenhado com um pequeno erro - 2-3 dezenas.
A régua "afrouxa" no suporte ao afrouxar a porca externa. Eu tenho esse pedaço de papelão debaixo do braço. Mas talvez apenas um parafuso.
Um pouco de geometria.
Todas as preparações listadas acima são necessárias para isso. Existe um conceito assim na geometria - um triângulo equilátero. Essa é uma figura geométrica que tem lados iguais e, portanto, ângulos iguais entre eles, ou seja, 60 graus. No nosso caso, o vértice do ângulo será o eixo do eixo da máquina, “materializado” na forma de um grampo de cabelo de 6 mm, no qual uma régua de um canto de alumínio é fixada. O triângulo, portanto, fica de lado. Desenhamos sua base na tela na forma de um acorde entre serifas no arco correspondente.
Como fazer isso?
Usando um lápis afiado e os segundo, terceiro, quarto e quinto orifícios da régua enfraquecida, desenhamos em uma folha de papel de arco.
Em seguida, meça 260 mm a partir do ponto inferior do arco externo, obtendo o segundo ponto (superior) da base do triângulo equilátero.
Por que no arco externo? É possível em qualquer um deles, mas quanto maior o raio, mais precisamente podemos marcar e desenhar um acorde - a base do triângulo. De fato, não há necessidade de desenhar uma linha de base: usaremos apenas serifas na curva, que são os vértices dos ângulos laterais do triângulo - os ângulos em sua base.
Podemos usar essa propriedade de um triângulo equilátero da seguinte maneira: nossa régua de um canto, abaixada até um suporte, está alinhada com um ponto da base do triângulo. Depois fixamos a régua com a chave, apertando a porca. Corremos o risco no painel frontal, escrevemos na fita adesiva a primeira marca - "O". Gire o cartucho manualmente até que a régua esteja alinhada com o segundo ponto da base do triângulo.
Assim, o painel frontal foi girado 60 graus. Fazemos uma marca no painel frontal com uma agulha e, na fita, escrevemos que é "60".
Em seguida, enfraqueça a porca que prende a régua, a régua desce "até a base", sem tocar no cartucho. Ou seja, a régua está novamente alinhada com o primeiro ponto da base do triângulo. Aperte a porca, privando a régua de mobilidade. Gire o mandril manualmente até que a régua esteja alinhada com o segundo ponto (superior) da base do triângulo. Nós corremos o risco no painel frontal, escrevemos na fita que é "120". E assim por diante, usando o mesmo algoritmo, marque o painel frontal com os rótulos "180", "240" e "300".
Como resultado, temos a oportunidade de dividir o círculo em 2, 3 e 6 partes.
Seguindo em frente. Precisamos colocar os riscos no painel frontal com uma divisão de 30 graus. Para fazer isso, a base do triângulo deve ser dividida ao meio. Como resultado, o ângulo de rotação da régua do ponto inferior para um novo ponto no meio da base será de 30 graus. Existem duas maneiras de dividir a base de um triângulo. Primeiro. Pegamos uma régua e, do ponto inferior da base, adiamos 130 mm, ou seja, metade do comprimento da base (acordes).
O segundo é geométrico. Pegamos a bússola e, com sua ajuda, depois de estender as pernas para um comprimento maior que a metade do comprimento da base (no meu exemplo, cerca de 150-160 mm), batemos em um ou no outro lado da base, sobrepondo o setor proposto com metade do comprimento da base. Em seguida, reorganizamos a agulha da bússola na parte superior do triângulo, sem alterar a distância entre as pernas da bússola, e corremos os mesmos riscos que devem se sobrepor aos das que foram desenhadas anteriormente. Nós conectamos os pontos resultantes e, na interseção desta linha com a linha de base do triângulo, será metade do comprimento dessa base.
E agora, usando o mesmo algoritmo, dividimos o painel frontal, causando divisões em 30 graus. Para fazer isso, combine qualquer um dos padrões aplicados anteriormente com a borda da régua superior. Enfraqueça a porca, abaixe a régua até o ponto inferior. Fixamos a porca, giramos o mandril para uma nova marca de 30 graus. Nós corremos o risco, escreva na fita adesiva a etiqueta correspondente. Por exemplo, se o risco de "120" foi combinado, girando o cartucho em uma direção no sentido horário, obteremos uma marca de 150 graus. E se você girar no sentido anti-horário, obtém 90 graus. E assim por diante, para todos os riscos recebidos anteriormente (marcas), até que o painel frontal esteja completamente preenchido com marcas com divisões de 30 graus.
Como resultado, temos a oportunidade de dividir o círculo em vários valores: em 4, 8 e 12 partes.
Agora, para finalizar a aplicação das divisões da escala principal, você precisa aplicar a divisão com um preço de 15 graus. Ou seja, setores de 30 graus devem ser divididos pela metade de qualquer maneira. Já passamos por isso, no sentido em que fizemos em setores de 60 graus. Então, temos marcas na tela com uma divisão de 15 graus e, com a ajuda deles, colocamos riscos no painel frontal.
Portanto, a escala principal está pronta, ou seja, uma escala com divisões ao preço de 15 graus.
Agora você precisa aplicar mais 4 escalas nessa escala principal para dividir em 60, 48, 42 e 36 divisões. Graficamente, fica assim:
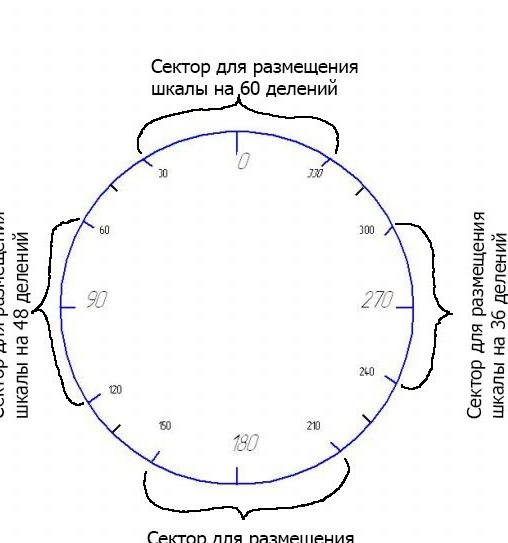
Coloquei as balanças nessa ordem. Mas você pode colocar qualquer uma dessas escalas em qualquer outro lugar, a seu critério. Achei esse canal mais conveniente. Observe que entre as escalas permaneceram setores intactos de 30 graus. Obviamente, você pode expandir os setores das escalas devido aos demais setores livres. Não fiz isso para não sobrecarregar a balança. Por exemplo, para uma escala de 42 divisões, 5 pontos a 8,57 por riscos de 180 em qualquer direção serão "defendidos" em 42,85 graus. Ou seja, quase perto das marcas 135 ou 245, o que pode complicar seu uso.
Parte 4. Desenhando uma escala de 60 divisões.
Para quebrar essa escala, precisamos obter divisões com um preço de 6 graus. Para fazer isso, novamente um pouco de geometria. Para obter um triângulo em um círculo com um ângulo no ápice de 6 graus, precisamos calcular o comprimento da base desse triângulo. O triângulo será equilátero, e a base do triângulo inscrita em um círculo é um acorde.
A fórmula para calcular o acorde é: L = 2 * R * sin (A / 2), L é o comprimento do acorde, R é o raio do círculo, A é o ângulo.
De todas as quantidades conhecidas por nós, sabemos apenas o valor do ângulo - 6 graus. Encontrar meio seno de 6 graus é uma questão de tecnologia.
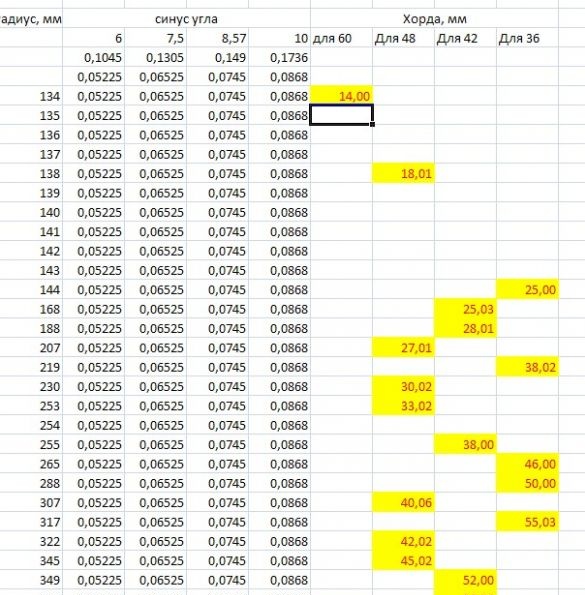
Fiz isso mais tarde: usei o método "puxão científico". Usando o programa Excel, uma tabela na qual incluí os comprimentos de raios com gradação de 1 mm a partir de 130. E de acordo com a fórmula, obtive os valores dos comprimentos de acordes. A tabela acabou sendo longa, parte dessa tabela após a exclusão de valores desnecessários (fracionários) ficou assim:
Resta selecionar os valores desejados. Como os cálculos foram feitos com precisão de 0,00001, escolhi, primeiro, mesmo os valores divididos por 4. Segundo, os que poderiam ser arredondados se não houvesse mais de 0,03 após o ponto decimal. Essa é a questão dos erros: não podemos "rastrear" três centésimos ao usar escalas. Deixe-me lembrá-lo de que a espessura da linha do lápis é de pelo menos 0,2 mm. Portanto, centésimos podem ser negligenciados com segurança (já estamos acostumados ao fato de sempre haver erros nas medições).
Por que é necessário "dividir" por 4? Mas simples. Afinal, primeiro dividimos a base do triângulo por 2 e depois novamente por 2. E, como resultado, obtivemos um número inteiro, não um fracionário.
A seleção de valores ficou assim:
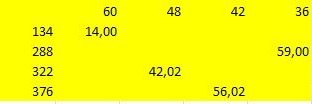
Mas então eu recusei essa escolha, já que entre 134 e 376 mm a diferença é muito grande. E procurou por outros significados. Encontrei. Eles não estão mais na mesa, porque Eu os cortei. Esses valores são 195.220.241 e 260 mm. Os arcos com tais raios estão localizados de maneira bastante compacta, sem interferir um com o outro. Sim, nem todo mundo é divisível por 4 sem deixar resto. E não precisamos de tudo. Para criar a escala principal, peguei o arco com o maior raio. Para dividir ao meio, usei o método gráfico, ou seja, usando uma bússola. E se você decidir usar uma régua, - uma bandeira em suas mãos!, - uma balança com um raio de 260 mm é dividida duas vezes ao meio sem deixar resto. Os comprimentos dos acordes são 34, 23, 36 e 34 mm, respectivamente.
Portanto, no setor para uma escala de divisão em 60 divisões, precisamos aplicar riscos com um preço de divisão de 6 graus. Como fazer isso? Tudo é simples, como um bipe de uma locomotiva a vapor. Usando uma régua ou bússola, adiamos um acorde de 23 mm de um ponto inferior ou qualquer outro ponto em um arco com um raio de 220 mm. O risco no painel frontal com um valor de "90" é combinado com a borda da régua superior. Combinamos a régua inferior com uma extremidade do acorde obtido, fixamos a porca, prendemos a régua. Giramos o cartucho para alinhar a borda da régua com a segunda extremidade do acorde. Tem um ângulo de 6 graus. Com uma agulha de bússola, corremos o risco no painel frontal. Para acelerar o processo (e reduzir pelo menos um pouco o número de erros de medição), é melhor usar a bússola para criar serifas não para um acorde, mas para vários. Então não será necessário afrouxar a porca de cada vez, para alinhar a régua com o ponto inferior, mas simplesmente após aplicar os próximos riscos, giramos o cartucho até os próximos riscos (final do próximo acorde).
Parte 5. As demais escalas.
O comprimento do acorde para uma escala de 36 divisões é de 34 mm, que, como antes, marcamos no arco, mas com um raio de 195 mm. Se você fizer 6 desses acordes, poderá começar a marcar a escala com o valor "240" e terminar com o valor "300". O preço de uma divisão é de 10 graus.
Além disso, de acordo com o algoritmo comprovado, usando um arco de 260 mm, a escala é dividida em 48 divisões (o comprimento do acorde é de 34 mm). O preço da divisão é de 7,5 graus.
Usando um arco de 241 mm, a escala é dividida em 42 divisões. O comprimento do acorde é 36 mm, o preço da divisão é 8,57 graus.
Conclusão
Mais uma vez sobre a pergunta: por que isso precisa complicar tanto a marcação? A resposta é simples: não preciso de você, não. Eu precisava de um colapso para fazer engrenagens com dentes para 42 e 48 dentes no futuro. Ainda precisa de escalas para 29 e 32 dentes. Mas eu os disponibilizarei com a ajuda de uma quebra temporária na fita. Mas será mais tarde.
E a última pergunta: como usá-lo, porque cada uma das escalas (exceto a principal) é curta, todo o segmento é 1/6 da circunferência da placa?
Resposta: fácil de usar. Vou mostrar um pouco mais tarde o vídeo (quando o montar). Enquanto isso, conte brevemente.
Você precisa colar a fita no cartucho. Em vez de um, você precisa assumir as duas principais réguas. É melhor com a galvanização, para que a régua possa ser facilmente dobrada.
E agora alguns exemplos. Digamos que precisamos marcar um círculo em 6 partes. Para fazer isso, use a balança principal, com uma régua superior. Combinando consistentemente os riscos de 0, 60, 120, 180, 240 e 300, obtemos uma divisão em 6 partes. O círculo, coma-mas, é preso no cartucho, que giramos e assumimos riscos ao longo da borda do cortador ou pelo próprio cortador.
Agora marque o círculo preso no cartucho em 5 partes. Não existem tais divisões na escala principal.Então, vamos pensar qual das escalas é divisível por 5 sem deixar resto? Verdadeiro: escala de 60 bar. Estas são 12 divisões. Mas caramba: temos apenas 10 divisões na balança !?
Calmamente, sem pânico. O preço de uma divisão desta escala é de 6 graus. Portanto, 12 divisões são 72 graus. E na escala principal do exemplo anterior, usamos setores de 60 graus. E o que nos impede de combinar uma linha superior com o risco de "300" e a outra linha para combinar no segundo risco à esquerda de "0". Ou seja, adicione 60 vezes 2 vezes a 6, obtemos 72. Posicionamos as réguas de forma que elas se ajustem perfeitamente no painel frontal. Não está funcionando É verdade que o raio do painel frontal é muito pequeno, a curvatura é grande e as réguas ficam suspensas no ar, ou elas precisam ser dobradas com força para que se encaixem perfeitamente no painel frontal. Não faça um ou outro. Basta ligar a cabeça e, em vez de 12 divisões, vamos usar 6 divisões, ou seja, 36 graus. E nos tornamos governantes através de 6 divisões.
Em fita com um lápis ou caneta, desenharemos traços nas réguas. Em nosso círculo, fazemos o primeiro entalhe com um cortador. Giramos o cartucho manualmente, digamos no decorrer do relógio, até que o traço esquerdo da fita adesiva fique alinhado com a borda da régua direita. Viramos 36 graus. Na fita na régua esquerda, desenhamos um risco e colocamos o cartucho nesse risco. Então, giramos 72 graus. Fazemos um segundo entalhe com um cortador. E assim por diante Uma sutileza. Traços com caneta ou lápis são "grossos", não importa o quanto você tente. Portanto, a borda da régua direita ao girar o cartucho não deve ser combinada com a borda direita da linha esquerda, mas com a borda esquerda. Ou seja, quase completamente a linha deve estar sob a régua certa. Caso contrário, um erro de 2 a 3 dúzias será acumulado a cada medição. E em um círculo, pode ser mais do que um milímetro.
Para dividir em 14 partes, você precisa usar uma escala de 42 divisões. 42: 14 = 3 divisões.
Mais interessante é a questão da quebra, suponha que para 144 partes. Não sei quem precisa, mas de repente? Aqui o algoritmo é diferente. Não temos escalas que seriam divisíveis por esse número. Então, não estamos procurando o número de entalhes, com graus de uma divisão. 360: 144 = 2,5 graus. Onde obter 2,5 graus? E se na nossa escala? !! Temos uma escala com um preço de divisão de 10 graus. E há uma escala com um preço de divisão de 7,5 graus. Se 10 - 7,5 = 2,5. Aqui está o resultado desejado! Como realizá-lo? A escala de 36 é levada ao topo, aos governantes. Combinamos uma régua com um risco da balança, outra com outra, com a mais próxima. Entre os governantes, temos um setor de 10 graus. Agora giramos o cartucho, elevando a escala para 48. O preço de suas divisões é de 7,5 graus. Combinamos um risco da balança, por exemplo, com a régua esquerda, na qual não tocamos. Em seguida, movemos essa régua para a segunda até que ela esteja alinhada com o risco mais próximo da escala em 48. Ou seja, reduzimos o setor de 10 graus em 7,5. No restante entre os governantes, temos um setor de 2,5 graus. E vai! Pelo mesmo princípio que ao dividir em 5 partes, usamos duas réguas.
Ok, outro exemplo. Suponha que você queira dividir um círculo em 40 partes. Contado: 360: 40 = 9 graus. Choramos - não temos essa escala! Vire a cabeça. Temos uma escala com um preço de divisão de 7,5 graus. Duas divisões nessa escala formarão um setor de 15 graus. Defina as réguas distantes umas das outras em duas divisões em uma escala de 48.
E agora dos 15 você precisa subtrair 6 para obter os 9 graus desejados. Onde temos 6? É isso mesmo, numa escala de 60. Já sabemos como fazer alguns graus usando as réguas. Marcamos.
Usando o mesmo princípio, um círculo pode ser dividido em 80 partes. 360: 80 = 4,5 graus. Três divisões em uma escala de 48 fornecerão 3 x 7,5 = 22,5. Três divisões em uma escala de 60 fornecerão 3 x 6 = 18 graus. 22,5 - 18 = 4,5.
E novamente para a teoria dos erros. Se você circula um grande número de padrões, o erro se acumula em cada marca. Para reduzir o erro, recomendo fazer metade das marcas. E depois volte ao começo e faça a marcação na outra direção, também à metade. Quando essas marcas "meia" convergem (e quase nunca convergem), veremos a magnitude do erro acumulado. Por exemplo, ao dividir em 8 partes, mostrei um erro na marcação de cerca de 0,1 - 0,2 mm. Para conexões rosqueadas, isso não é crítico: as roscas nos parafusos sempre falham sempre em 3-4 dezenas. Mas se eu seguisse a marcação sequencialmente, a magnitude do erro poderia aumentar para 0,5 mm, e isso é muito.A conclusão da teoria dos grandes números: quanto menos medições fizermos, menos nos enganaremos. E vice-versa, quanto mais medições, mais erros se acumulam. Isso deve ser levado em consideração.